During my dynamics class, I became particularly bothered by the treatment of frames of reference. We always did our analysis from a "ground frame", which produces counterintuitive behavior. For example, we can imagine two particles moving parallel to each other, both at the same constant velocity. With the typical approach, each particle has an angular momentum about the other. This didn't sit right with me, as from the particle frame of reference, there is no relative motion to each other–they are both sitting completely still. Why should they have an angular momentum relative to each other in the ground frame if they have no relative velocity?
An easy way to resolve this is to apply the regular formulation from an inertial frame moving with the particles. However, from this frame now, any two particles at rest in the ground frame would have an angular momentum about each other despite having no relative velocity.
I therefore set out to derive my own equations, but with the constrain that angular momentum about an origin should only depend on the relative velocity of origin and particle. I extended this to rigid bodies and yielded the same equations of motion as the "ground-frame" formulation for example problems (always good!). It's also, in my opinion, more intuitive and oftentimes quicker (example demonstrating this at top of 4th page). Finally, it's possible to solve problems using both formulations, as shown by the equations boxed in blue along the middle of the pages.
In short, by choosing a frame which "follows" the origin, we ensure that only velocities relative to the origin are considered. In order to use this frame, though, we must account for the fictitious forces that arise from being in an accelerated frame. Because the center of mass is not necessarily at the origin, these fictitious forces act with a moment arm from our origin, therefore producing a "fictitious torque" about the origin.
Another concept I initially struggled to accept was the instantaneous center of rotation (ICR) in no-slip rolling. There are two common approaches to solving these problems: one treats the ICR as a material point—a point on the body that has zero velocity at a given instant—while the other treats it as a geometric point that continuously traces the contact location with a non-zero velocity. The lack of a clear distinction between these two interpretations bothered me, so I tried solving problems both ways. An example of a rolling object on a ramp, analyzed with both resulting methods, in both formulations is on page 4. In hindsight, I’m not entirely satisfied with my early attempts—I feel I steered the logic towards a known result, even if the physics doesn't clearly imply the step. Over the summer, I revisited the problem with a more rigorous approach to treating the ICR as a material point: by expressing the point’s position for a small time interval before it becomes the ICR. This method feels much more consistent, though there’s still plenty left to explore. An example of this method, which yields the correct equation of motion for an example problem of a particle on a rocking chair is shown at the bottom of page 4.

pg. 1
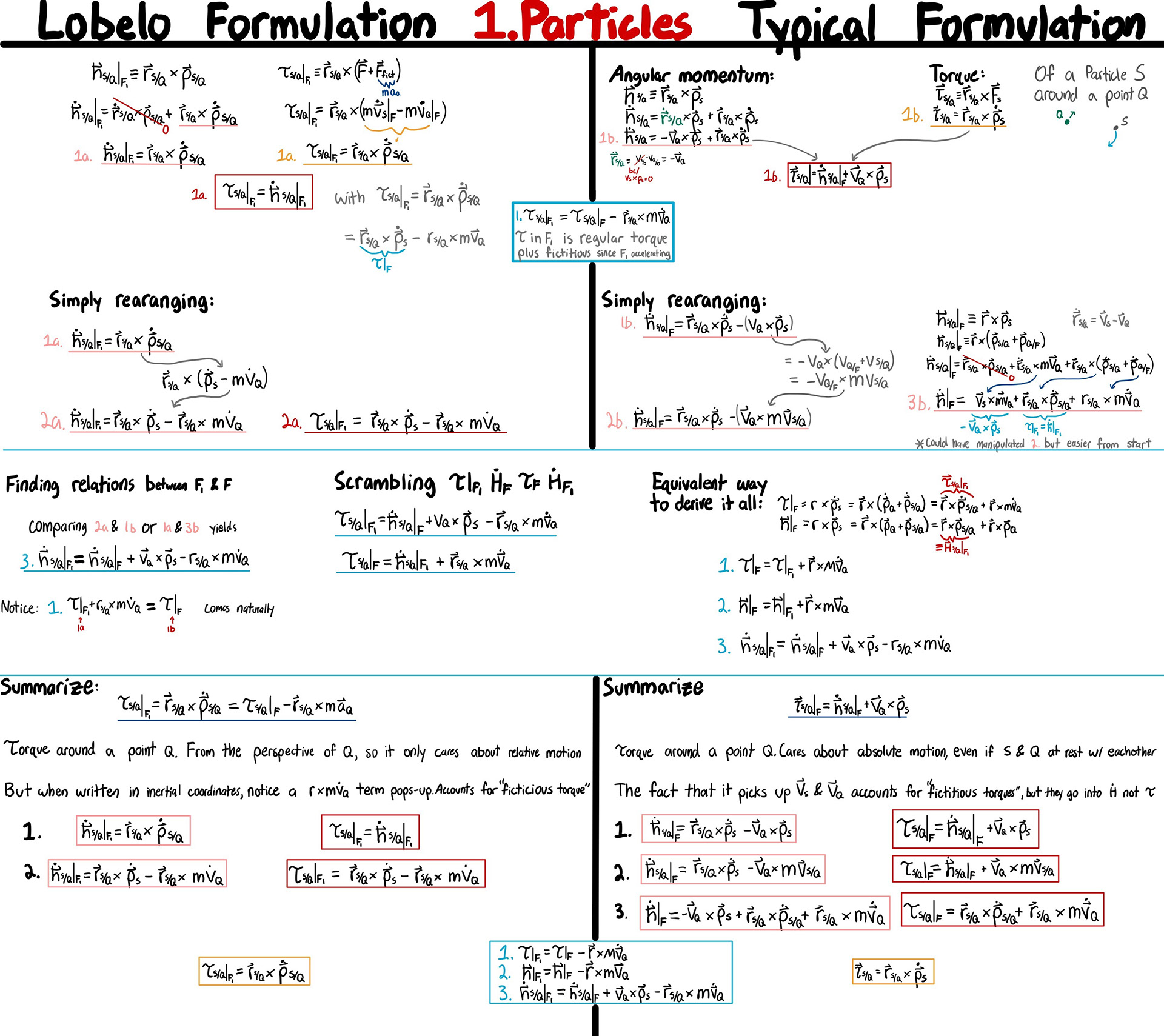
pg. 2
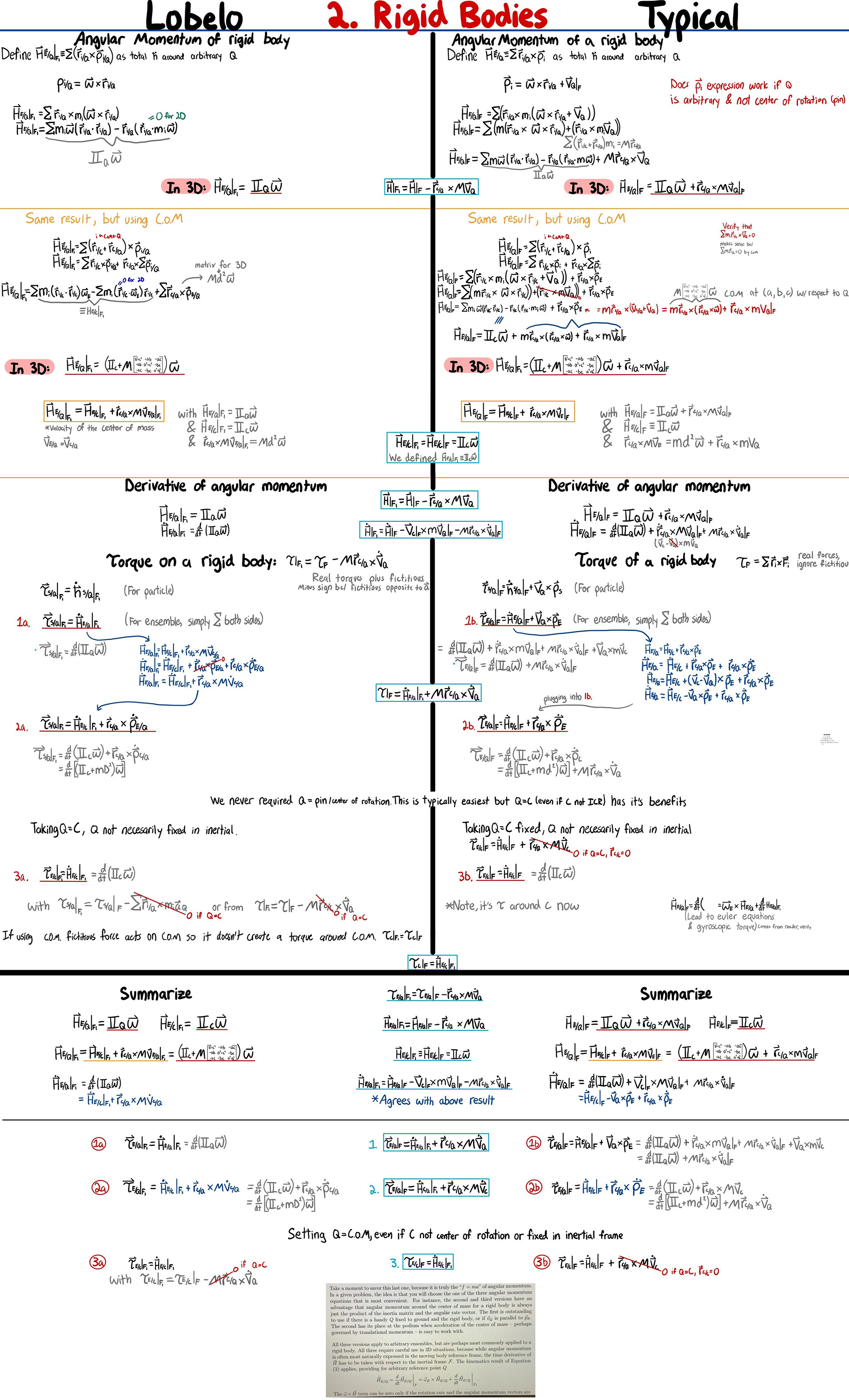
pg. 3
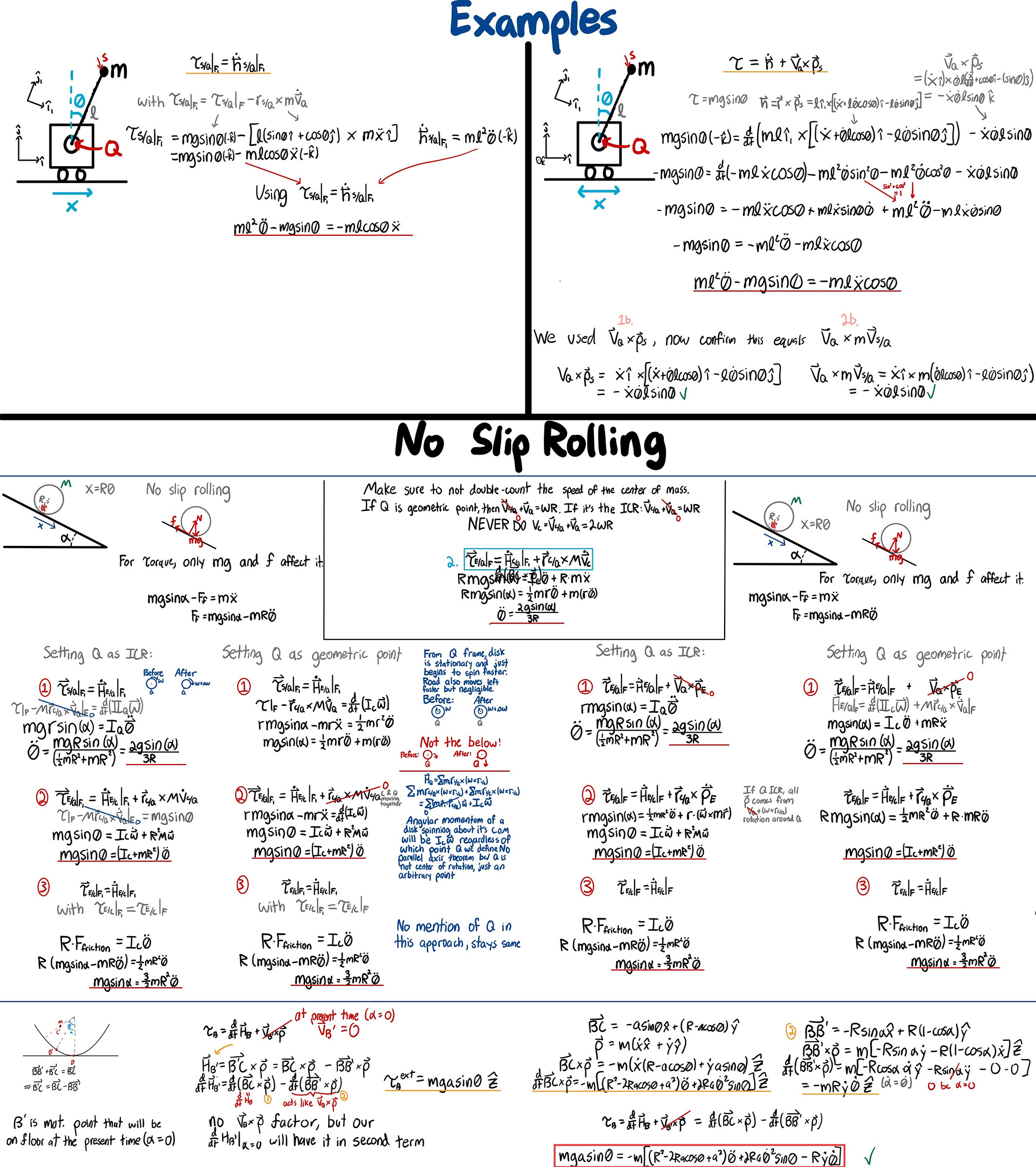
pg. 4
Now I'm working to extend my formulation to include its own "energy-method," way to solve dynamic problems with energy only works in inertial frames.